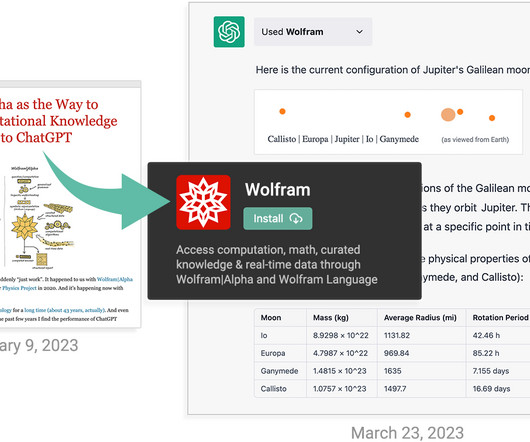
ChatGPT Gets Its “Wolfram Superpowers”!
Stephen Wolfram
MARCH 23, 2023
And in the end, as we’ll discuss later, that’s a more flexible and powerful way to communicate. But then mathematical notation was invented, and math took off—with the development of algebra, calculus, and eventually all the various mathematical sciences. But it doesn’t work unless the Wolfram Language code is exactly right.









Let's personalize your content